Larry Ellison's Driveway (a.k.a. CS270 Project)
Project History
As the project progressed, the requirements changed. The final
requirements are in the next section.
This section briefly outlines the steps by which we arrived at the
final requirements.
Background
A friend of mine is an architect working for the lead contractor for
Larry Ellison's new house. Part of the project involves designing his
driveway, including the access roads. Ellison wants the driveway to
look like a tradition cut-stone driveway. However, both he and the
lead architect want to see the design before it is built. Also, the
stones are to be cut in Japan, and then shipped to the US.
My friend was assigned the job of designing the driveway. Faced with
the task of producing about 40,000 stone drawings, he estimated it
would take 6 months of work. I suggested that a computer program could
generate the stone drawings directly. He agreed.
(Note: Due to time constraints on his project, Larry
Ellison did not end up using this for driveway. I believe he did use
it for some bridges and walls, however.)
Initial Requirements
Initially, the problem was posed as follows:
- Each stone should be unique.
- The area of each stone must be within a range (about 2 square feet).
- The number of sides of the stones should vary from 5 to 9.
- Angles should not be too acute.
- Concave or convex stones are allowed.
One of the first attempts was to construct a Voronoi diagram with
random control points. Although this produces only convex polygons,
and does not guarantee any of the constraints, it provides a starting
point. The following figure consists of 200 randomly chosen points
forming a Voronoi tessellation of a 100x100 plane.
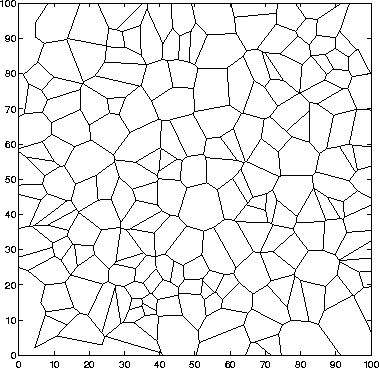
A Random Voronoi Tessellation
The response from the lead architect upon seeing this picture was that
it was "too random". He wanted it to be closer to a grid. This led to
a second approach, namely, starting with a rectangular grid of points,
perturbing the points, and forming a Voronoi tessellation from the
result. The amount of randomness can be controlled with a single
parameter v, the mean amount of perturbation (from a normal
distribution).
The next three images show the result with v = 0.1, 0.15, and
0.2.
v = 0.10 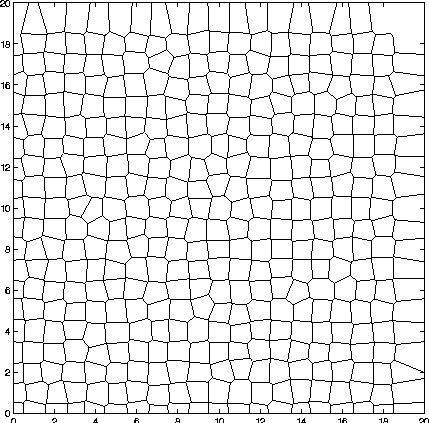
v = 0.15 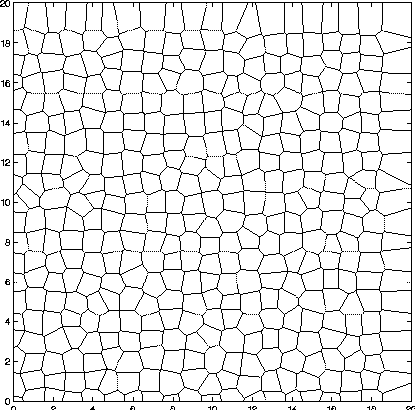
v = 0.20 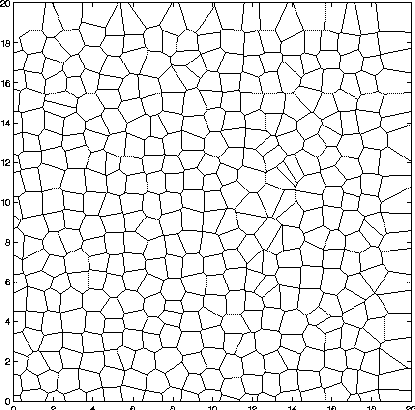
The center image, with v = 0.15, was the most preferred.
After this iteration, I spent more time getting the detailed
requirements nailed down, including looking at examples (mostly of
walls rather than driveways) that were close to what they were looking
for. Almost all the requirements changed at least a bit.
- The requirements on the area of a stone turned out to be related
only to the weight. If the stones got too big, they would be too
difficult to ship. However, for aesthetic reasons, they wanted the
stones to be approximately the same size.
- The constraints on the number of sides turned out to be very
loose. As long as it looked good, the details were not important.
- The angle constraints were to prevent thin protrusions of stone,
which might break during shipping.
- In the examples, all the stones were convex.
The stones generated by the Voronoi tessellation of a perturbed grid
appeared to satisfy the modified constraints.
The final change in the requirements came up once the architects had
spoken directly with the stone masons. Although a computer could
easily generate the forty thousand or so stone designs, the
stone masons absolutely refused to cut that so stones to order. They
placed a limit of about 50 total distinct stone designs.
This change led to the final requirements as outlined in the
next section.
Prev TOC Next
Adam Janin
janin@icsi.berkeley.edu




