
The Meeting Recorder project involves making recordings of multi-participant meetings simultaneously through head-mounted microphones and 'ambient' microphones on the conference table. One long-term goal is to develop speech recognition for ambient recordings, and towards this end we would like to compare the ambient mic signals with best-case signals derived from the head-worn mics. We are also using the head-worn mics as the source material for transcriptions made for our data by human transcribers.
The image below gives an illustration of the nature of the data. The overall energy for six simultaneously-recorded channels is shown for a three-minute extract from one of our recordings. The top band comes from one of the ambient (PZM) mics; the remaining five bands are five head-worn mics, the last of which is actually a lapel mic, which can be seen to have picked up more background noise than the others (or perhaps it is just recorded at a higher level - it's hard to say). Gray scale in the image shows the energy variation over a range of about 50 dB.
(Click on the image to hear the PZM channel audio, which picks up all the speakers).
In the image, we see that initially Jerry is speaking, up to t= 688 sec, then Mark speaks through to t=780 s, then Nancy speaks. In each case, occasional back-channel utterances are made, e.g. by Jerry during Mark's monologue at t=765 s. We also see that there is a considerable variation in energy in all the channels even when the speaker concerned is silent. This is correlated across channels, and also correlates with the active speaker i.e. it is the bleed-through cross-talk of the active speaker being recorded by the headset mics of the other participants, albeit at a lower level. The PZM channel, however, seems to be picking up a high level of background noise that is not obviously correlated with the other channels. This may be low-frequency noise from the air conditioning to which the head-mounted mics do not respond.
There are a couple of things we might want to do with this data. Firstly, we would like to do some preliminary speech activity detection in each channel to come up with a 'template' of speech events at particular times in particular channels to give our transcribers a starting point. We could even run a first-pass recognition to give the transcribers guesses at the words, but that would probably be more distracting than useful. However, opening the transcription interface with appropriate time points already set and correctly assigned to particular speakers would certainly speed things up. Even if the speech activity detection is not completely accurate, the transcribers can remove any obvious errors as they are entering the text.
The second obvious post-processing for this data is to do actual signal cancellation between the channels to obtain waveforms that, as much as possible, consist only of a single person's speech. While in the example above there is only one speaker at any time for the bulk of the time, there are several instances of simultaneous speech (particularly the brief utterances referred to as backchannel above), and it will help in our baseline recognition performance if we can eliminate this cross-talk as much as possible. We should be in a good position to do this - we have as many or more microphones than sources (in most cases), and each source is dominant in one of the channels. However, we do need to estimate the frequency-dependent coupling function between the channels, which may have a fairly long impulse response depending on the reverberation of the room, and will vary with time as speakers move. See the less-than-perfect results below.
For the energy envelopes as shown in the image above, we are going to assume a simple, linear, instantaneous mixing that generates the observed microphone signals from the ideally-separated sources, i.e. m = C.s + n, where m is a column vector of observed microphone signals at a particular time, s is the vector of ideal source energies at that time, n is a vector of noises added to each observation, and C is the mixing matrix. If we assume that we are observing N microphones recording N sources, then C is square at NxN.
This is a classic blind signal separation problem, and we could approach it by searching for the inverse mixing matrix C-1, by doing gradient descent to maximize the correlation between nonlinear functions of the output signals [Bell & Sejnowski 1995; Amari et al 1996]. However, for our first task of simply identifying the episodes of when each participant speaks (so that we can create a transcription template), we don't so much care about the shape of the source signals themselves, but just which source it is i.e. which channel is active.
Let us assume that, in most conditions, there is only one speaker active. This means that all but one of the elements of s is zero, and, ignoring the effects of the noise n, the observed microphone signals are just a scaled copy of the corresponding column of C. In the log domain (e.g. when measured in dB), this means that each channel is moving up and down at the same rate, determined by the single excitation source to which all channels are responding, and the only difference between channels is a fixed offset corresponding to the log of the coupling gain i.e. log(mi) = log(sj) + log(cij) .
In practice, it is not that clean. Firstly there is background noise in the recordings, contributing an excitation which is not like the well-behaved point-source of a particular speaker. Background noise may be more or less correlated between different channels (depending on whether it originates within or near the microphone, or elsewhere), but in any case will have a different pattern of coupling. Secondly, the single scalar coupling gain we are discussing is actually the net result of applying a frequency-dependent channel to a source excitation with a rapidly-varying spectrum. As the source speech shifts is spectral concentration between bands of high and low coupling, the observed overall energy coupling will fluctuate.
However, ignoring these complications for the moment, we can form an estimate of the excitation energy envelope, without knowing which channel it is in, simply by averaging the log energies of all the channels, which should then give log(sj) + mean(log(cj)), where sj is the active source, and cj is the j'th column of C. If we then subtract this average from each of the individual observed channels, we should be able to factor out the excitation, and be left just with the cij terms reflecting the relative coupling of the particular active source - which we would expect also to be dominated by the channel corresponding to the head-mounted mic for the current speaker. The result of this processing is shown in the next figure:

Through this processing, much of the frame-to-frame variation has indeed been removed, although not all, perhaps partly due to the inclusion of the noise-dominated PZM channel in the average. (In this particular meeting there were in fact participants who were not wearing headsets, so one reason for the PZM being included in this processing is in the hope of capturing their utterances too).
Also notice that, although Nancy's speech at t=785 s is probably easier to pick out in this display, the contrast between her 'active' and silent channel energy is much smaller (about 5dB) than for Jerry and Mark (who seem to manage10dB or more). This is due to the different properties of her lapel mic, as mentioned above, providing less of a gain advantage for her speech over the other speakers.
The other processing used to the data in the figure is an effort to remove the systematic offsets between the channels, specifically the higher overall levels in the PZM channel and on Nancy's lapel mic. One approach would me to remove the mean level from each channel, but this would have the undesirable effect of subtracting more from a channel containing a lot of speech activity (such as Mark) than from a relatively infrequent speaker (such as Andrea, in the figure anyway). What we really want is to align the 'noise floor' in each channel, the level when the corresponding speaker is not active. To this end, I subtracted the minimum energy observed in each channel, which, assuming the behavior during quiet periods is about the same, should normalize channel gains. This is why the dB scale in this graph is all positive, and much higher than the range in the raw energy figure.
Having conditioned the data to exhibit a clearer and better-defined distinction between activity and silence in each channel, the next problem is to make an automatic classification of these different episodes. The simplest approach is to find a threshold energy to apply to excitation-normalized channels that separates the two modes. However, given the differences in channel properties (due to differences between speakers and variations in microphone positioning etc.), this threshold may be different for each channel. We would like to be able to derive the threshold for each channel.
To choose a threshold, a good place to start is the histogram of energy levels. The figure below shows the energy histograms for some of the channels in the raw energy figure. We see a typical one-tailed distribution in most channels, with a more symmetric distribution for the PZM channel. In the case of Mark, we can vaguely see a bimodal distribution, the upper mode presumably corresponding to his active regions, but the separation between silent and active is very blurred. For Nancy, no upper mode is evident at all.
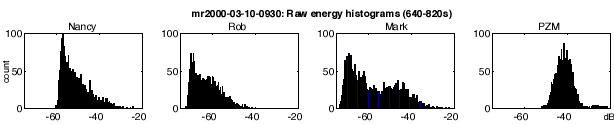
Constructing histograms of the excitation-normalized energies is more helpful, as shown below. Now the two modes in Mark's channel are much better defined, and the 'active' mode in Nancy's channel is pretty clear too.

The remaining problem is to define an automatic algorithm to find a threshold between the two modes in channels like Mark's and Nancy's, while still behaving reasonably on channels that have very little activity, such as Rob's, or that may not fit the bimodal assumption at all, such as the PZM channel.
The basic approach I took was to use the EM algorithm to describe each distribution as the sum of several Gaussians. Gaussians are initially placed arbitrarily, then re-estimated based on a soft assignment of data points to the nearest Gaussian components. Empirically, the fitting took about 30 iterations to converge, but each step is rather fast. This approach has been used in very similar situations for SNR estimation, when a single channel needs to be divided into 'signal' and 'noise' regions so their ratio can be estimated. After experimenting with a variety of configurations, the best approach seemed to be to use 3 Gaussians, and to use the upper edge of the middle Gaussian (i.e. mean + 3 sds) to define the threshold between the lower-energy 'background' and the more energetic 'active' regions. This particular solution probably reflects that every individual channel spends more time silent than active. (I also had to add a fudge so that if the 'middle' Gaussian is very broad, but the upper one is more concentrated, the sd used in calculating the threshold is taken from the upper Gaussian).
The figure below shows the results of this threshold-setting algorithm for three of the channels. In each case, the histograms are overlaid with the three EM-derived Gaussians, with the 'middle' Gaussian drawn in red, and the derived threshold shown as a green line. Taking Jerry's channel first, we see the 'classic' behavior, with the low-energy mode being modeled by two of the Gaussians, and the high-energy, active mode modeled by the third Gaussian. Using the upper edge of the low mode gives a very plausible threshold location. Looking next at Nancy, we see that the Gaussian model has behaved a little differently for a channel with a smaller proportion of active frames: the highest Gaussian actually straddles both her active mode and some of the inactive energy. This is why we use the upper edge of the assumed inactive mode rather than the lower edge of the active mode to set the threshold. Finally, for Rob, who has very little activity in the modeled region, we see that all three Gaussians are modeling the single mode, but again choosing the upper eedge of the 'middle' Gaussian again gives a good estimate of the upper limit of this main mode, allowing us to label the few instances of unusually high energy as active. Sorting the Gaussians into bottom, middle and upper was done via mean+sd rather than mean alone, so that the broader Gaussians sometimes used to cover the upper tail of the distributions would be correctly considered as 'upper', even if their means were essentially the same as the others.
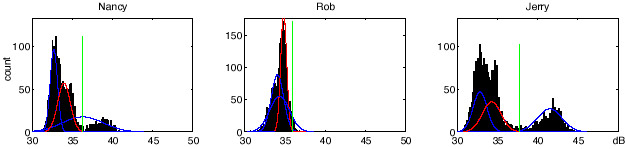
Thus, we obtain a fixed energy threshold for each excitation-normalized channel. By comparing the actual channel levels to this threshold, we can obtain binary 'activity masks' for each channel in the segment, as shown below. These can then serve as the basis for our 'activity template' to seed the transcriptions i.e. for each region of activity, we assume there should be a corresponding lexical transcription to fill in.

Comparing this to the energy plots above, it appears that we have done a reasonable job detecting the main speech regions, even for the low-activity channels of Rob and Andrea. For the PZM channel, it's not clear if there is any significant energy to be detected, and probably most of the indicated events are spurious. For the purposes of seeding the transcriptions, however, it's probably better to overproduce and have the transcribers delete or ignore the superfluous placeholders, than to miss candidate events altogether.
I have yet to actually derive transcript templates from these data. In that step, it will be useful to apply some smoothing, ignoring short pauses in active speech sequences, and perhaps filtering out some of the isolated peaks. It may help to use something more sophisticated than applying a single threshold, such as using hysteresis via two thresholds, perhaps on a smoothed version of an upper-bounded version of the excitation-normalized channel energies. (Upper-bounding will prevent a large but short-duration transient, such as inadvertent contact with a microphone, from being smoothed to spread out to a plausible utterance duration).
Given decisions about when each source is active, it should be relatively trivial to recover the mixing matrix C of our original mathematical model. If we ignore the noise added to each channel, we could simply average the across-channel profile for the frames labeled as containing activity from a particular source, to recover (to within a scale factor) the column ofC relating to that source (as presented above). To be a little smarter about possible uncorrelated noise sources, we could find the covariance between other channels and the presumed 'direct' source again over the frames for which that source (alone) is active. Thus if sj is the only nonzero source,
mi = cij.sj + ni
so
E[mi.mj] = E[cij.sj.cjj.sj + cij.sj.nj + cjj.sj.ni + ni.nj]
and if we assume that the noises are uncorrelated with the source and each other, this reduces to
E[mi.mj] = E[cij.cjj.sj ^2]
If we then define cjj to be unity, and assume that nj is absorbed into cj, we have
cij = E[mi.mj] / E[mj^2]
By considering the active regions of each channel separately (as estimated in the previous section, though over a longer chunk of the signal, to ensure some activity for every channel), we can get an estimate C' for the whole of C, and we can then attempt to recover the energy envelopes of the original sources as
s' = inv(C').m
where the multiplication is performed in the linear-energy-envelope domain (although it might be better to do it in the intensity-squared i.e. power domain, since uncorrelated signals add linearly in the power domain).
Using this approach, we can readily recover estimates of the separate source envelopes exciting each channel once we have estimated C. The results of this calculation are shown in the figure below:

Although it's a little hard to tell with the different way that the grayscale has mapped out, this appears to have improved the contrast between activity and silence in each channel when compared with the raw energy. However, it doesn't provide any obvious improvement over the simple average-channel normalization originally tried, and it suffers from a couple of problems. Firstly, the PZM channel now has lots of excitation, presumably because the PZM had low correlation with the other channels, so ended up with small mixing coefficients. Secondly, events which depart from the usual mixing profile, such as the transient near t =730 s (which arises when Mark breathes out suddenly, causing breath noise in his microphone) now get spread from a single channel to lying across all channels. Thus mixing inversion doesn't seem as an attractive approach for activity detection. However, doing full-up blind signal separation on the individual waveforms (rather than on the energy envelopes) would offer the hope of recovering actual isolated source waveforms, which would be useful for recognition, and is thus worth pursuing.
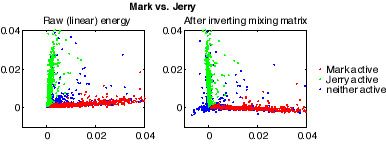
Just to get a concrete sense of what the mixing inversion is doing, here are scatter plots for the energy in Mark's channel versus that of Jerry. Red points correspond to times where Mark was labeled as active; green are Jerry active, and blue are neither of them active. The plot on the left is the original channel energies (on linear scales), clearly showing the correlation caused by the coupling between the channels. The right plot shows the results of decorrelation, which do indeed rotate the main lobes to be close to uncorrelated, although in the process some of the 'energies' are reduced below zero, which doesn't make sense computationally (these values are clamped to zero in the figure above). Note that the 'main lobes' of the scatter plots now appear to have a slight negative correlation. This I believe is because of the few outliers, points labeled as 'Mark active' which actually have significant energy in Jerry's mic (resulting e.g. from some background noise local to Jerry) which then skews the overall distribution. More careful EM-style relabelling of the active region labels for each speaker should be able to eliminate this.
Back to DAn's Meeting Recorder page - DAn's homepage - ICSI Meeting Recorder homepage - ICSI Realization group homepage